Metodo de asignaciòn

El problema de asignación tiene que ver con la asignación de tareas a empleados, de territorios a vendedores, de contratos a postores o de trabajos a plantas. Al aplicar el método de transporte y el método de asignación la gerencia está buscando una ruta de distribución o una asignación que optimizará algún objetivo; éste puede se la minimización del costo total, la maximización de las utilidades o la minimización del tiempo total involucrado.

Al igual que el método de transporte el método de asignación es computacionalmente más eficiente que el método simplex para una clase especial de problemas. El método de asignación también conocido como la Técnica de flood o el método Húngaro de asignación.

Hay básicamente tres pasos en este métodoDetermine la tabla de costo de oportunidad:Reste el elemento del costo más bajo en cada columna de la tabla de costo dada, de todo los elementos en esa columna.

Reste el asiento más bajo en cada renglón de la tabla obtenida en la parte 1.1 de todos los números en ese renglón.

Determine si se puede hacer una asignación óptima: El procedimiento es dibujar líneas rectas (verticales y horizontales) a través de la tabla de costos total de oportunidad, de tal manera que se minimice el número de líneas necesarias para cubrir todos los cuadros CERO.

Si el número de líneas dibujadas es menor que el número de renglones o columnas, no se puede hacer una asignación óptimas y el problema no está resuelto.Revise la tabla de costo total de oportunidad.

Seleccione el número más pequeño en la tabla no cubierto, por una línea recta y reste este número de todos los números no cubiertos por una línea recta.Añada este mismo número a los números que están en la intersección de dos líneas cualesquiera.

Regrese al paso 2 .

Metodo dual

A cualquier problema que llamamos primal tiene mas restricciones que variables, esto simplifica la solución porque el problema se representa como un problema dual y se maneja con menos restricciones.Esto es:1.- si el primal se refiere a maximizar, el problema dual sera minimizar.2.- los coeficientes de la funcion objetivo del primal seran los coeficientes del vector de disponibilidad de recursos en el dual.3.- asi, los coeficientes del vector disponibilidsd de recursos del problema primal seran los coeficientes de la funcion objetivo (vector costos, precios o utilidad) en el programa dual.4.- los coeficientes d e las restricciones en el primal ( transpuesta de la matriz), sera la matriz de los coeficientes tecnológicos en el dual.5.- los signos de desigualdad del problema dual son contrarios a los del primal.6.- las variables “x” del primal, se convierten en nuevas variables “y” en el dual.

1.- considerando el siguiente problema primario, calcular su modelo dual.Sea máx. = Z= 3x + 5y

Ponemos los coeficientes disponibilidad en forma de vector columna ( matriz) primal

y estos se convierten en vector, horizontal o vertical ( matriz fila ) transpuesta; esto es

Hacemos las restricciones del primal en forma de matriz

Por lo tanto su transpuesta Dual Sera:

Y al maximizar:

Metodo Vogel

Es un método de ahorro que trabaja sobre el ahorro y suele producir una mejor solución óptima o próxima al nivel óptimo.

Paso 1.-Requiere de una penalización para cada renglón (columna)
Restando el menor elemento de costo del renglón

Problema:

Supongamos que a una empresa transnacional que tiene tres plantas R , S, T estas surten de producto hacia almacenes A , B , C, D, E, F, G, que forman parte del grupo empresarial debemos considerar lo relacionado al costo de transporte desde la planta a cada almacén.

Prueba de optimidad

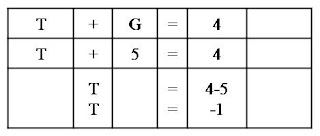
Conclusiones

Metodo de las dos fases

Este método elimina el uso de la M y resuelve el problema en dos fases. En la fase I se utiliza el algoritmo simplex para suministrar a la fase II una forma factible de partida. Es decir, el producto final de la Fase I es una solución básica factible (en caso de que exista), en forma típica, para iniciar la Fase II del método. Los pasos de cada fase son lossiguientes:

Fase I
1. Utilice el algoritmo simplex para obtener la minimización de la suma de las variables artificiales, sujeta a las mismas restricciones del problema original, independientemente de si este problema original es de maximización o minimización.

2. Si la suma de las variables artificiales, X0, es mayor que cero, entonces no existe una solución básica factible y se termina el proceso. Si X0= 0, entonces inicie la Fase II del algoritmo.

Fase II
1. Utilice la solución óptima obtenida en la Fase I como solución de partida al problema 1. original, remplazando la función objetivo original Z por la de X0. Como es usual, la función objetivo original debe ser expresada en función de las variables no básicas. Si al final de la Fase I las variables artificiales son no básicas, se eliminan de la Fase II. Si alguna variable artificial es básica, pero a un nivel cero, esta variable se mantiene en el conjunto de variables básicas, pero debe garantizarse que su valor nunca será mayor que cero durante la ejecución de la Fase II. Ejemplo:

MIN W = 3 X1 + 4 X2

Resolver el anterior problema de Programación Lineal por el Método de las Dos Fases.
Solución analítica:

Fase I :
Paso 1 Se introducen las variables artificiales A1 y A2, las variables de exceso S1 y S2.

MIN X0 = A1 + A2

Con sus restricciones:

FASE I:
Puesto que A1 y A2 son variables básicas, sus coeficientes en la fila X0 deben ser cero (0); para ello sumamos las filas (1) y (1) a la fila (0). El tablero inicial para la aplicación del algoritmo simples es:

TABLERO 1 SIMPLEX
0
0
Cj
0
0
0
0
1
1
CB
VB
B
X1
X2
S1
S2
A1
A2
1
A1
20
2
3
-1
0
1
0
1
A2
30
1
5
0
-1
0
1
0
X0
50
3
8
-1
-1
1

1 Entra a la base X2 y sale de la base A2

VB
VNB

A1 = 20A2 = 30 X1 = 0X2 = 0S1 = 0S2 = 0 X0 = 50

TABLERO 2 SIMPLEX
CB
VB
b
X1
X2
S1
S2
A1
A2
1
A1
2
7/5
0
-1
3/5
1
-3/5
0
X2
6
1/5
1
0
-1/5
0
1/5
0
X0
2
7/5
0
-1
3/5
1

-3/5 Entra a la base X1 y sale de la base A1 VB VNB A1 = 2X2 = 6X1 = 0A2 = 0S1 = 0S2 = 0X0 = 2

TABLERO 3 SIMPLEX
CB
VB
b
X1
X2
S1
S2
A1
A2
0
X1
10/7
1
0
-5/7
3/7
5/7
-3/7
0
X2
40/7
0
1
1/7
-2/7
-1/7
2/7
0
X0
0
0
0
0
0
0
0

Al aplicar el método simplex a nuestro problema en la tercera etapa de la fase I se ha encontrado que mín X0 = 0 y no existen variables artificiales en la base. Por lo tanto, se ha encontrado una solución básica posible al problema original.FASE II:

Empleamos la función objetivo original W en lugar de X0 y eliminamos las variables artificiales A1 y A2, puesto que ya no son variables básicas, es decir, son variables no básicas. Como la función objetivo debe estar expresada en términos de las variables no básicas, entonces se deben realizar transformaciones para reducir a cero el coeficiente de X1 y X2 en la función objetivo.

TABLA

Ejercicios de transporte

PROBLEMA 1

Tres plantas de producción P1, P2 y P3 con capacidades de 100000, 100000, y 150000, respectivamente, tienen que abastecer cuatro ciudades C1 ,C2, C3 y C4, que demandan 50000, 70000, 60000 y 80000 unidades, respectivamente. Los costes de producción por unidad de cada planta son de 1 u. m., y los costes asociados al transporte por unidad se reflejan en la siguiente tabla:

Desarrollar un programa lineal que permita determinar el número de unidades que deberá producir cada planta y cuál será el plan de transporte que minimice los costes totales de la operación.


PROBLEMA 2
Una empresa suministra patatas a cuatro mayoristas cuyas demandas respectivamente son 100, 75, 50 y 125 toneladas. Dispone de tres almacenes, en diferentes puntos, cuyas capacidades son 150, 100 y 50 toneladas. Si los costos de distribución, en miles de pesetas por tonelada, de cada almacén a cada mayorista son:



Formular un programa lineal que permita calcular la política de distribución óptima sabiendo que por cada tonelada de demanda insatisfecha la empresa tiene unas pérdidas de 20000, 25000, 20000 y 15000 pts. respectivamente.


PROBLEMA 3

Una empresa se dedica a recoger y comercializar naranjas. Estas son recogidas, empaquetadas y trasladadas a uno de los almacenes que la empresa posee en Tampa, Miami y Fresno. Desde estos almacenes, a su vez, se transportan las naranjas a los mercados de Nueva York, Filadelfia, Chicago y Boston.

En el cuadro siguiente se muestran los costes de transporte por tonelada ($) y los requerimientos máximos de demanda y oferta de los mercados y de los almacenes:



Formular un programa lineal que permita a la empresa saber qué política de transporte debe aplicar, de tal modo, que el coste sea mínimo.

Modelo de transporte

Este modelo trata, básicamente, de encontrar las mejores formas o rutas para el traslado de las mercancías, desde “n” orígenes hasta “m” destinos, para sus diferentes de almacenamiento, buscando la forma de minimizar los costos de transporte.

CONDICIONES:

1.-Tanto la función objetivo como las restricciones deben ser lineales
2.-Las mercancías a distribuir deben ser uniformes, así como los coeficientes de las variables en las restricciones deben ser 0 o 1.
3.-La suma de la capacidad de todos los orígenes debe ser igual a la suma de la capacidad de los destinos. En otras palabras, la demanda total tiene que ser igual a la oferta total.

m: Es el centro de la oferta
n: Es el centro de demanda
( i ): Renglón por cada origen
( j ): Cada destino una columna
Ai: No. De unidades disponibles en cada centro de oferta
bi: No. Requerido de unidades de mercancía en el centro de demanda
Cij: Costo unitario de transporte en la ruta de un centro de oferta a un centro de demanda.
Xij: Cantidad transportada del centro de oferta al centro de demanda.



CASO PRÁCTICO
Supongamos que a una empresa trasnacional que tiene 3 plantas W, X, e Y, y estas surten de un producto a 7 almacenes: A,B,C,D,E,F,G que forman parte del grupo empresarial, debemos considerar lo relacionado al costo de transporte desde cada planta a cada almacen. También, sabemos que cada almacén tiene ciertos requerimientos de ventas, mismas que dependen de la capacidad de cada planta.Veamos en la siguiente tabla las capacidades de producción mensuales, los requerimientos de ventas por mes y los costos de transporte de cada planta hacia cada almacén.Queremos determinar la ruta de distribución menos costosa y el costo total mínimo.

(m= renglones, n= columna; m+n -1 = No. De casillas asignadas; 3 + 8 -1 =10)

Metodo SIMPLEX por minimizaciòn

Minimizar Z= 3m + 4n - 8ñ

3m – 4n ≤ 12
M + 2n + ñ ≥ 4
4m – 2n +5ñ ≤ 20

M ≥ 0, n ≥ 0, ñ ≥ 0

Como es un problema de minimización recordemos que tenemos que maximizar la función objetivo quedando así

-3m – 4n + 8ñ + Z = 0

Las inecuaciones las hacemos igualdades

3m – 4n = 12
m + 2n + ñ = 4
4m – 2n +5ñ = 20

Ahora tenemos que hacer nuestra tabla 1 y aplicaremos el mismo procedimiento del método SIMPLEX para maximizarlo


Ahora de la tabla tomaremos el MAYOR POSITIVO en este caso es el 8 y ya encontramos nuestra columna pivote.

Posteriormente dividimos 28/5 = 4 4/1 = 4 12/0 = 0, y tenemos que tomar el numero menor de estas divisiones en este caso tenemos dos, cuatros podemos tomar cualquiera

Y ya encontramos nuestro pivote operacional en este caso es 1, ahora tenemos que dividir toda esa fila entre este 1 para poder resolver la siguiente tabla



Ahora la ñ ya paso a la base

El problema se termina aquí porque ya nos quedaron puros negativos y ceros en nuestra PO que era nuestro objetivo

3m – 4n ≤ 12
3(0) – 4 (0) ≤ 12
0 ≤ 12 Si cumple

m + 2n + ñ ≥ 4
0 + 2(0) + ¼ ≥ 4
¼ ≥ 4 No cumple

4m – 2n + 5ñ ≤ 20
4 (0) – 2 (0) + 5 (1/4) ≤ 20
1.25 ≤= 20 Si cumple

3m + 4n – 8ñ
Z = 3 (0) + 4(0) – 8 (1/4)
Z = 2

Metodo de la M

Este método empieza con la PL en la forma estándar Para cualquier ecuación i que no tiene una holgura, aumentamos una variable artificial R. Entonces esta variable se convierte en parte de la solución básica inicial. Debido a que es una variable artificial al modelo de PL se le asigna una penalidad en la función objetivo, para obligarlas aun nivel cero en una iteración del algoritmo SIMPLEX

Debido a que M es un valor positivo suficientemente grande, la variable R1 se penaliza en la función objetivo utilizando —MR, en el caso de la maximización, y +RM, en la minimización. Debido a esta penalidad El proceso de optimización lógicamente tratara de impulsar R1, al nivel cero

Minimice Z= 4X1 + X2

La forma estándar se obtiene restando un superávit X3 en la segunda restricción y añadiendo una holgura X en la tercera restricción. Por tanto obtenemos

La primera y segunda ecuación no tiene variables que desempeñen el papel de holguras. Por consiguiente, utilizamos las variables R1 y R2 en estas dos ecuaciones y las penalizamos en la función objetivo con MR1 + MR2. La PL resultante se da como


En el modelo modificado, ahora podemos utilizar R1, R2 y X4 como la solución básica factible inicial como lo demuestra la siguiente tabla simplex

Antes de proceder con los cálculos del método simplex, necesitamos hacer que el renglón -Z sea consistente con el resto de la tabla simplex. De manera específica, el valor de z asociado con la solución básica inicial R1 = 5, R2 6, y X4 = 4 debe ser 3M + 6M + O = 9M en vez de O, como se muestra en el lado derecho del renglón -Z. Esta inconsistencia se debe al hecho de que R, y R2 tienen coeficientes no cero (-M, -M) en e! renglón -Z Estas inconsistencias se eliminan sustituyendo R1 y R2 en el renglón -Z, utilizando las ecuaciones apropiadas de restricción.

En particular, observe los elementos “1” realzados en el renglón -R1 y en el renglón -R2. Multiplicando cada uno de los renglones –R1 y de los renglones -R2 por M y añadiendo la suma al renglón -Z, efectivamente se sustituirá a R1 y R2 en el renglón objetivo. Podemos resumir este paso como

Nuevo renglón Z= Antiguo renglón Z + M x (Renglón R1) + M x (Renglón R2)
Esto se aplica como

Por lo tanto la nueva tabla simplex se convierte en

2 TABLAS



La solución óptima es:

X1= 2/5; X2= 9/5; X3= 13/5; Z = 17/5