2), que es el óptimo. Obsérvese que el procedimiento no es capaz de cortar a través del espacio de soluciones (por ejemplo, de A a C) sino que siempre debe moverse a lo largo de bordes entre puntos extremos adyacentes.
¿Cómo se expresa algebraicamente el procedimiento iterativo indicado antes? Todo foque tenemos que hacer es mostrar cómo se identifican los puntos extremos, tales como el A, B y C, sin utilizar la gráfica de] espacio de soluciones. Consideremos el modelo Reddy Mikks dado enseguida en su forma estándar:
Maximizar Z= 3x5 + 2x1 + Os3 + 0.s + Os, + 054

sujeto a

El modelo tiene m = 4 ecuaciones y n = 6 variables. De esta manera, el número de variables no básicas (nulas) debe ser igual a 6 — 4 = 2. Si escogemos e, O y x, = O como las variables no básicas, inmediatamente, y sin ningún cálculo, obtenemos la solución básica factibles1 = 6, .s5 = 8, s3 = 1 54 = 2 (el punto origen A en la figura 3-1). Esta solución básica representa la solución inicial (o iteración) del método símplex. El valor objetivo correspondiente se determina expresando la función objetivo en la siguiente forma (a la que nos referiremos como la ecuación z):
8 — 3X — 2.r1 = O
Puesto que x5 y x1 en A son cero, el valor asociado de z lo da automáticamente el segundo miembro de la ecuación anterior (= O). La fácil determinación algebraica de la solución básica inicial en el modelo Reddy Mikks se debe a que:
1. Cada ecuación tiene una variable de holgura.
2. Los segundos miembros de las restricciones son no negativos.
La primera propiedad garantiza que el número de holguras es igual al número de ecuaciones. Así, las variables restantes pueden usarse como variables no básicas (cero). Como por la segunda propiedad los segundos miembros de las ecuaciones son no negativos, la solución básica resultante es automáticamente factible, como se necesita en el método simplex primal.
El siguiente paso lógico a la identificación de la solución inicial, es investigar el desplazamiento a una nueva solución básica. Desde el punto de vista de la optimización, nos interesa pasar a otra solución básica, sólo si podemos discernir mejoras en el valor de la función objetivo. Primero, téngase en cuenta que una nueva solución básica se asegura sólo al hacer básica, por lo menos, una de las variables actuales no básicas (cero). En el método símplex se hace el cambio de las variables no básicas, una a la vez, Intuitivamente, tal variable no básica puede llevarse a a solución sólo si mejora el valor de la función objetivo, En términos del modelo Reddy Mikks, .r y x son no básicas (= O) en A. Observando la ecuación z objetivo
z—3x—2x, O
constatamos que un incremento unitario de x aumentará a z en 3 y, un incremento unitario dex1, acrecentará a z en 2. Puesto que se trata de una maximización, cualquiera de las dos variables puede mejorar el valor objetivo. Sin embargo, para generar una regla no ambigua de cálculo, el método simplex utiliza un procedimiento heuristico; osca, en el caso de una maximización, la variable no básica seleccionada es aquella con el coeficiente más negativo en la ecuación z objetivo. Utilizando tal procedimiento heurístico, se espera (pero no se garantiza), que el método símplex produzca los ‘saltos” máximos en el valor objetivo al pasar de una iteración a otra, alcanzando así el óptimo en el menor número de iteraciones. La aplicación de esta condición al modelo Reddy Mikks da como resultado considerar a como la variable que entra, o variable entrante.

Condición de factibilidad: tanto en problemas de maximización como de minimización, la variable saliente es la variable básica actual, con la menor intersección (razón mínima con denominador estrictamente positivo) en la dirección de la variable entrante. Un empate se rompe arbitrariamente.
Estamos listos para enunciar los pasos iterativos formales del método símplex primal:
Paso O: Usando la forma estándar (con los segundos miembros no negativos), determine una solución inicial básica factible.
Paso 1: Seleccione una variable entrante entre las variables actuales no básicas, usando la condición de optimidad.
Paso 2: Seleccione la variable saliente entre las variables actuales básicas, usando la condición de factibilidad.
Paso 3: Determine los valores de las nuevas variables básicas, haciendo a la variable entrante básica y a la variable saliente no básica. Vuelva al paso 1.
Ejemplo 3.3-1
Usaremos el modelo Reddy Mikks para explicar los detalles de cálculo del método simplex primal. Esto exigirá expresar el problema en la forma estándar Una manera conveniente de resumir las ecuaciones es por medio de la siguiente tabla:
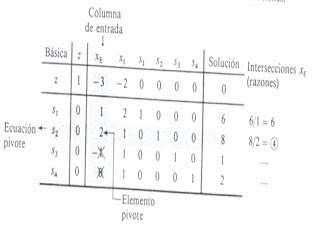
Esta tabla corresponde a la solución básica inicial del modelo. La información en la

Tabla se lee de la siguiente manera. La columna “básica” identifica las variables básicas actuales y’, s,, y, y y4, cuyos valores se dan en la columna “solución”. Esto supone implícitamente que las variables no básicas y5 y y, (aquellas no presentes en la columna “básica”) tienen valor cero. El valor correspondiente de la función objetivo es Z = 3 x O + 2 x o + Ox 6 + Ox $ + Ox 1 + Ox 2 = O, como se muestra en la columna solución.
Al aplicar la condición de optimidad, tiene el coeficiente más negativo en la ecuación a y por ello, se escoge como la variable entrante. La condición de factibilidad muestra que .5 corresponde a la menor intersección, por lo que deberá salir de la solución.
Después de identificar las variables entrantes y salientes, necesitamos determinar la nueva solución básica que debe incluir ahora a y,, y5, y, y 54 Esto se logra aplicando el método de eliminación de Causs-1ordan. El método comienza identificando la columna debajo de la variable entrante y5 como la columna entrante o de entrada. El renglón asociado con la variable saliente se denominará ecuación pivote, y el elemento en la intersección de la columna de entrada y la ecuación pivote se denominará elemento pivote. La siguiente tabla resume estas definiciones:
No hay comentarios:
Publicar un comentario